As mentioned in Scaling Vs Normalization, applying normalization to the input features increases the convergence rate of our algorithm i.e. it speeds up the learning process.

In deep neural networks, you not only have input features but activations in the hidden layers also. Can/Should you normalize them also? The answer is Yes. Normalizing the inputs to hidden layers helps in faster learning. This the core concept of batch normalization.

It’s called “batch” normalization because, during training, we normalize each layer’s inputs by using the mean and standard deviation (or variance) of the values in the current batch

In simple terms, in batch normalization, rather than just performing normalization once in the beginning, you’re doing it all over the network. But, normaliztion will squeeze your values to [0, 1]. It’s not desirable always. So, you apply \(\gamma\) and \(\beta\) parameters to your normalization value. These parameters are learned the same way as other hyperparameters through backpropagation during the training process.

Hence, batch normalization ensures that the inputs to the hidden layers are normalized, where the normalization mean and standard deviation are controlled by two parameters, \(\gamma\) and \(\beta\).

Why does batch normalization work?

Now, coming to the original question: Why does it actually work?

Suppose you train a neural network on the images of black cats only. Then your model won’t perform well on different colored images of cats. The reason is the shift in the input distribution. This is known as covariate shift. The covariate shift is the change in the distribution of the covariates i.e. predictors or input variables. Batch normalization reduces this covariate shift.

The internal covariate shift refers to the change in the distribution of the inputs to different layers. It turns out that training a network is most efficient when the distribution of inputs to each layer is similar!

The idea is that even when the exact values of inputs to hidden layers change, their mean and standard deviation will still almost remain same thus reducing the covariate shift. This weakens the coupling between parameters of early layer and that of later layers hence, allowing each layer of the network to learn by itself i.e. more independent of each other. This has the effect of speeding up the learning process.

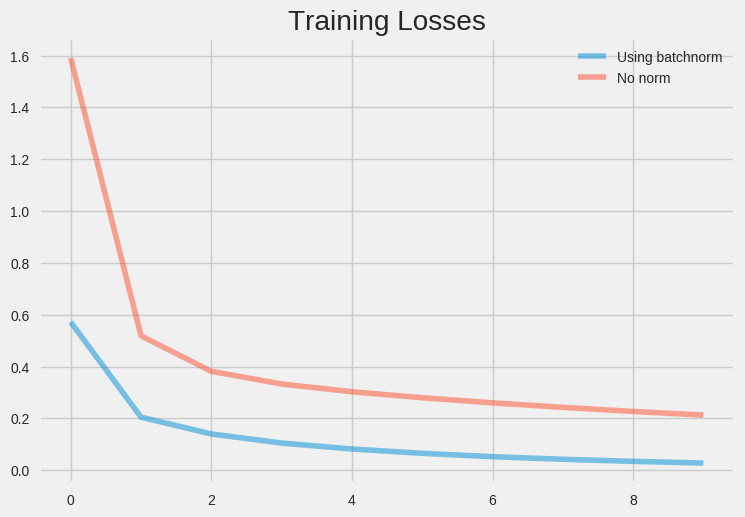
The other benefit of batch normalization is that it acts as regularization. Each mini-batch is scaled using its mean and standard deviation. This introduces some noise to each layer, providing a regularization effect.

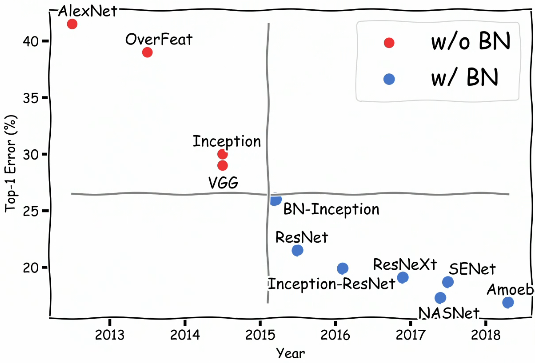
Due to numerous benefits of batch normalization, it’s extensively used nowadays as evident from the below figure.

References:

1. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
2. Batch norm usage (Image source)