False positive paradox
Friday, October 12, 20182 mins read
A false positive is an error when test results incorrectly indicate presence of a condition when it doesn’t exist. False positives often plays an important role in hypothesis testing, especially in testing of rare diseases. Sometimes, it happens that the test having low probability of giving false positive gives more false positives than true positives overall. This is called false positive paradox.
Let’s take an example to understand this.
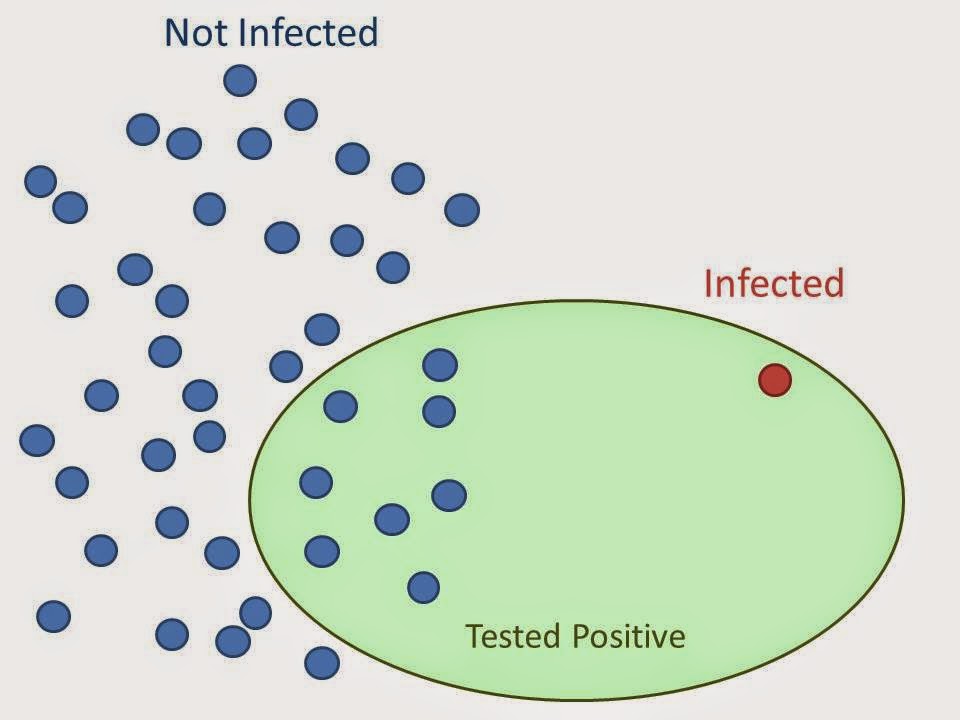
The test results of a rare disease in a population A, in which 40% people are infected, are as follows:
| A | Test negative | Test positive | Total |
|---|---|---|---|
| Infected | 570 (TN) | 30 (FP) | 600 (N) |
| Uninfected | 0 (FN) | 400 (TP) | 400 (P) |
| Total | 570 (N *) | 430 (P *) | 1000 |
Here, the false positive rate is FP/N = 570/600 = 93% and the accuracy of the test is (TP+TN)/N = (400+570)/1000 = 97%.
The same test when applied to the population B, in which only 2% are infected, gives following results:
| B | Test negative | Test positive | Total |
|---|---|---|---|
| Infected | 931 (TN) | 49 (FP) | 980 (N) |
| Uninfected | 0 (FN) | 20 (TP) | 20 (P) |
| Total | 931 (N *) | 69 (P *) | 1000 |
Here, the false positive rate is 20/69 = 29%; the accuracy of the test is (20+931)/1000 = 95%
Thus, a person having a positive test result in A will have 93% chances that he/she is infected. On the other hand, the same person having positive test result after takes the same test in B will have only 29% chance of being infected for a 95% accurate test.
So, in a society with very few infected people—fewer proportionately than the test gives false positives—there will actually be more who test positive for a disease incorrectly and don’t have it than those who test positive accurately and do.
These results seems to be a paradox. The probability of a positive test result is determined not only by the accuracy of the test but by the characteristics of the sampled population also. But if you look closely and don’t judge a test based only on its accuracy, you will know that it’s not a paradox but simple statistics even though it may seem counter-intuitive.
The false positive paradox is a type of base rate fallacy, where our mind tends to ignore the base information such as population and focuses on the specific information such as accuracy. These paradox arises due to a flaw in our reasoning that violates principles of probability such as Bayes theorem.
References: