Evaluation metrics for classification and False positives
Friday, December 29, 20173 mins read
A false positive error or false positive (false alarm) is a result that indicates a given condition exists when it doesn’t.
You can get the number of false positives from the confusion matrix. For a binary classification problem, it is described as follows:
| Predicted = 0 | Predicted = 1 | Total | |
|---|---|---|---|
| Actual = 0 | True Negative (TN) | False Positive(FP) | N |
| Actual = 1 | False Negative (FN) | True Positive (TP) | P |
| Total | N * | P * |
In statistical hypothesis testing, the false positive rate is equal to the significance level, \(\alpha\), and \(1 - \alpha\) is defined as the specificity of the test. Complementarily, the false negative rate is given by \(\beta\).
The different measures for classification are:
| Name | Definition | Synonyms |
|---|---|---|
| False positive rate (\(\alpha\)) | FP/N | Type I error, 1- specificity |
| True Positive rate (\(1-\beta\)) | TP/P | 1 - Type II error, power, sensitivity, recall |
| Positive prediction value | TP/P* | Precision |
| Negative prediction value | TN/N* | |
| Overall accuracy | (TN + TP)/N | |
| Overall error rate | (FP + FN)/N |
Also, note that F-score is the harmonic mean of precision and recall.
\[\text{F1 score} = \frac{2 * \text{precision} * \text{recall}}{\text{precision} + \text{recall}}\]For example, in cancer detection, sensitivity and specificity are the following:
- Sensitivity: Of all the people with cancer, how many were correctly diagnosed?
- Specificity: Of all the people without cancer, how many were correctly diagnosed?
And precision and recall are the following:
- Recall: Of all the people who have cancer, how many did we diagnose as having cancer?
- Precision: Of all the people we diagnosed with cancer, how many actually had cancer?
Often, we want to make binary prediction e.g. in predicting the quality of care of the patient in the hospital, whether the patient receive poor care or good care? We can do this using a threshold value \(t\).
- if \(P(poor care = 1) \geq t\), predict poor quality
- if \(P(poor care = 1 < t\), predict good quality
Now, the question arises, what value of \(t\) we should consider.
- if \(t\) is large, the model will predict poor care rarely hence detect patients receiving the worst care.
- if \(t\) is small, the model will predict good care rarely hence detect all patients receiving poor care.
i.e.
- A model with a higher threshold will have a lower sensitivity and a higher specificity.
- A model with a lower threshold will have a higher sensitivity and a lower specificity.
Thus, the answer to the above question depends on what problem you are trying to solve. With no preference between the errors, we normally select \(t = 0.5\).
Area Under the ROC Curve gives the AUC score of a model.
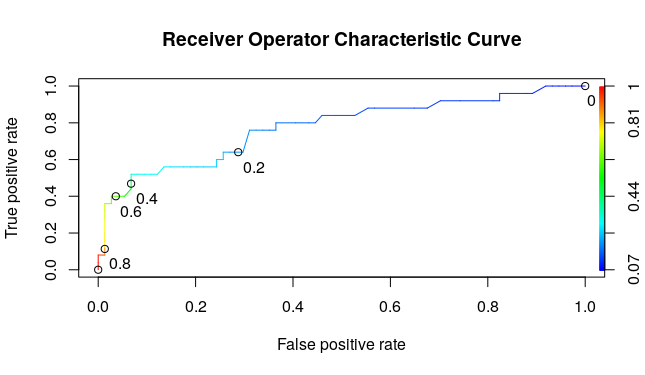
- The threshold of 1 means that the model will not catch any poor care cases, or have sensitivity of 0 but it’ll correctly label all the good care cases, meaning that you have a false positive rate of 0.
- The threshold of 0 means that the model will catch all of the poor care cases or have a sensitivity of 1, but it’ll label all of the good care cases as poor care cases too, meaning that you’ll have a false positive rate of 1.
Below is xkcd comic regarding the wrong interpretation of p-value and false positives.

Explanation of above comic on explain xkcd wiki.
References: