In supervised learning, we have data x and response (label) y and the goal is to learn a function to map x to y e.g. regression, classification, object detection; while in unsupervised learning, there are no labels and the goal is to find some underlying hidden structure of the data e.g. clustering, dimensionality reduction, feature learning. The goal of generative models is to generate new samples of data from a distribution. These models are used in problems such as density estimation, a problem of unsupervised learning.

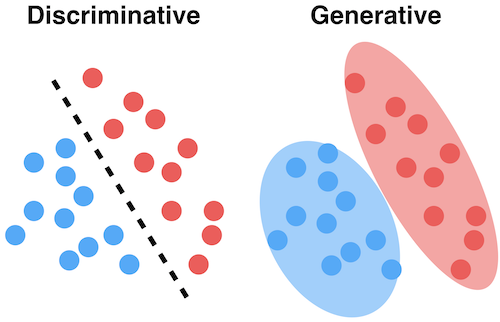
Generative model Vs Discriminative model

The discriminative models learn the conditional probability distribution \(P(y \mid x)\) i.e. the decision boundary between classes e.g. logistic regression, neural network. The generative models learn the joint probability distribution \(P(x, y)\) i.e. the distribution of individual classes e.g. naive Bayes, Gaussian discriminant analysis (GDA).

Generative Adversarial Networks (GAN)

Suppose you want our network to generate images as shown:

You can use GAN to achieve so. The idea is to take sample from a simple distribution (such as random noise, Gaussian distribution) and learn transformation (parameters of model) to true distribution.

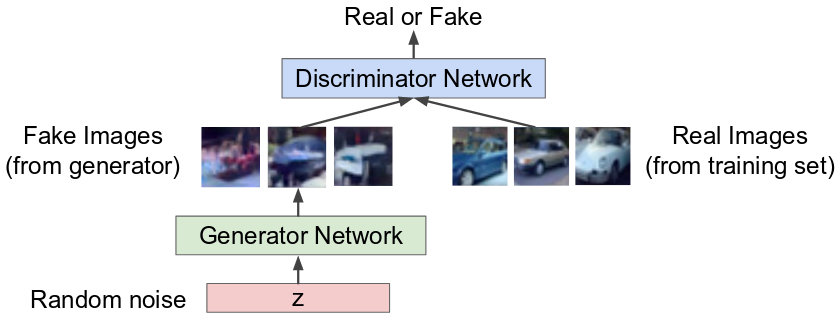
GANs were invented by Ian Goodfellow et al. in 2014 in Generative Adversarial Nets. It has two networks, competing with each other:

• Generator try to fool the discriminator by generating real-looking images
• Discriminator try to distinguish real images from the fake ones generated by the Generator

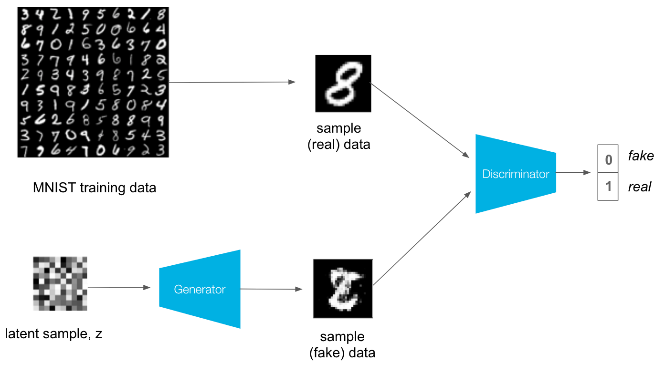
Training

Training involves alternating between training the discriminator and the generator. The real loss and fake loss are used to calculate the discriminator losses as follows.

Discriminator (D) training

For the real images, we want D(real images) = 1. That is, we want the discriminator to classify the the real images with a label = 1, indicating that these are real. The discriminator loss for the fake data is similar. We want D(fake images) = 0, where the fake images are the generator output, fake_images = G(z).

1. Compute the discriminator loss on real, training images
2. Generate fake images
3. Compute the discriminator loss on fake, generated images
4. Add up real and fake loss to get total loss
5. Perform backpropagation + an optimization step to update the discriminator’s weights

Generator (G) training

The generator’s goal is to get D(fake images) = 1.

1. Generate fake images
2. Compute the discriminator loss on fake images, using flipped labels.
3. Perform backpropagation + an optimization step to update the generator’s weights

\(D(G(z))\) is the probability that the output of the generator G is a real image. \(D\) and \(G\) play a minimax game in which D tries to maximize the probability it correctly classifies reals and fakes \((logD(x))\), and G tries to minimize the probability that \(D\) will predict its outputs are fake \((log(1−D(G(x))))\). The GAN loss is defined as:

After training the network, we can remove the discriminator and use generator network to generate new images.

There are many other types of generative models such as PixelRNN and PixelCNN, Variational Autoencoders (VAE).

References:

1. Generative Adversarial Nets
2. Generative Learning algorithms - CS229
3. Generative models - OpenAI
4. Image source - Discriminative Vs Generative
5. Image source - CS231n
6. GAN hacks