Matrix Multiplication in CUDA
Friday, June 7, 202420 mins read
Matrix multiplication is at the heart of deep learning. In this evolving world of LLMs, the need for fast and efficient matrix multiplications is paramount. Nvidia CUDA allows you to perform matrix operations on GPU in a faster way.
CUDA (Compute Unified Device Architecture) is a parallel computing platform and application programming interface (API) model. CUDA programming model provides an abstraction of GPU architecture (API for GPUs).
In this blog post, we will explore how to implement matrix multiplication using CUDA. We will start with a naive implementation on the CPU and then demonstrate how to significantly speed up the process using CUDA.
Naive C++ Implementation on CPU
Since in most hardwares, matrices are stored in row-major format, let’s define our 2d matrices as row-major 1d arrays.
struct Matrix
{
int height;
int width;
float *elements; // height x width
// you can also use std::vector<float> elements for automatic memory management
};Matrix multiplication for computing each element of matrix C from matrices A and B can be written as follows:
where i and j are the row and column indices of the resulting matrix C and k is the index used for the summation over the common dimension.
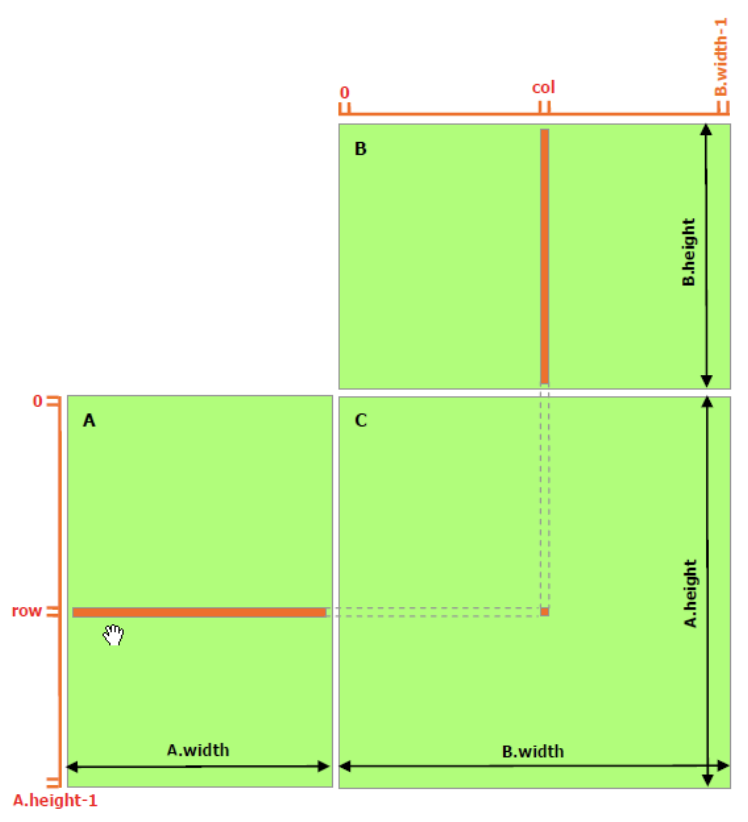
Our naive matrix multplication in C++ on CPU is:
void matMulCPU(const Matrix &A, const Matrix &B, Matrix &C)
{
for (int row = 0; row < A.height; ++row)
{
for (int col = 0; col < B.width; ++col)
{
float cValue = 0;
// C[i][j] = sum_k A[i][k] * B[k][j]
for (int k = 0; k < A.width; ++k)
cValue += A.elements[row * A.width + k] * B.elements[k * B.width + col];
C.elements[row * C.width + col] = cValue;
}
}
}We can use the below main() function to call our matMulCPU() and measure its performance.
// Function to initialize a matrix with random values
void initializeMatrix(Matrix &mat)
{
for (int i = 0; i < mat.height * mat.width; ++i)
mat.elements[i] = static_cast<float>(rand() % 100);
}
int main()
{
int M = 1024; // Rows of A and C
int K = 768; // Columns of A and rows of B
int N = 1024; // Columns of B and C
// Allocate matrices A, B, and C
Matrix A = {M, K, new float[M * K]}; // 1024x768
Matrix B = {K, N, new float[K * N]}; // 768x1024
Matrix C = {M, N, new float[M * N]}; // 1024x1024
// Initialize matrices A and B with random values
initializeMatrix(A);
initializeMatrix(B);
// Measure the time taken for matrix multiplication on the CPU
auto start = std::chrono::high_resolution_clock::now();
matMulCPU(A, B, C);
auto stop = std::chrono::high_resolution_clock::now();
std::chrono::duration<float> duration = stop - start;
cout << "CPU matrix multiplication time: " << duration.count() * 1000.0f << " ms" << endl;
// Clean up memory
delete[] A.elements;
delete[] B.elements;
delete[] C.elements;
return 0;
}Naive CUDA Kernel
In CUDA, we define a CUDA kernel, which is a function (e.g. C++ function) executed by CUDA.
In CUDA programming model, there is a three-level hierarchy. The threads are the smallest unit of execution. These threads are grouped into a CUDA thread block. CUDA blocks are grouped into arrays called grids. The kernel is written from the perspective of a single thread in CUDA. Thus, a kernel is executed as a grid of blocks of threads.
On a CPU, matrix multiplication is typically performed sequentially, where each element of the output matrix is computed one after another. This process can be slow for large matrices due to the limited number of CPU cores available for parallel execution. In contrast, the GPU excels at parallel processing. A CUDA kernel is executed by many threads running simultaneously, allowing for significant speedup in computations like matrix multiplication. The GPU’s architecture enables it to handle thousands of threads concurrently, making it well-suited for tasks with high levels of parallelism.
Let’s re-write the above matrix multiplication code in CUDA. We use __global__ keyword to define a CUDA kernel. Here, we assign a thread for calculation of each element of output matrix C. And, multiple such threads are run in parallel. Each thread reads one row of A and one column of B to compute one element of C.
Threads and blocks are indexed using the built-in 3D variable threadIdx and blockIdx. The blockDim gives the dimension of thread block. We can access index using dot attribute e.g. threadIdx.x, threadIdx.y, and threadIdx.z. Thus, for 2d thread block, we can access particular element of C using a combination of these as shown in below code.
__global__ void matMulNaiveKernel(Matrix A, Matrix B, Matrix C)
{
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
// Each thread accumulates one element of C by accumulating results into cValue
float cValue = 0;
// C[i][j] = sum_k A[i][k] * B[k][j]
// Iterates over common dimensions of A and B (k = A.width = B.height)
if (row < A.height && col < B.width)
{
for (int k = 0; k < A.width; ++k)
cValue += A.elements[row * A.width + k] * B.elements[k * B.width + col];
C.elements[row * C.width + col] = cValue;
}
}We create a 16x16 thread block (256 threads with 16 each in x and y-direction). We define (B.width/BLOCK_SIZE, A.height/BLOCK_SIZE) blocks per grid. Extra operations below is to take care of the last tile if size isn’t perfectly divisible.
#define BLOCK_SIZE 16
dim3 threadsPerBlock(BLOCK_SIZE, BLOCK_SIZE);
dim3 blocksPerGrid((B.width + threadsPerBlock.x - 1) / threadsPerBlock.x,
(A.height + threadsPerBlock.y - 1) / threadsPerBlock.y);
runKernel(matMulNaiveKernel, A, B, C, blocksPerGrid, threadsPerBlock);This kernel is called with device (gpu) matrices A, B, and C as follows:
kernel<<<blocksPerGrid, threadsPerBlock>>>(d_A, d_B, d_C);This setup ensures that the CUDA kernel efficiently processes the entire matrix by dividing the workload among the available threads and blocks.
To execute CUDA program:
- Copy the input data from host (cpu) memory to device (gpu) memory. This is called host-to-device (H2D) transfer.
- Run CUDA kernel on data.
- Copy the results from device memory to host memory, also called device-to-host (D2H) transfer.
We pass our kernel to the runKernel() function that also takes CPU matrices A and B. It copies the data from CPU to GPU, runs kernel, copy result from GPU to CPU, and return the result matrix C.
void runKernel(void(*kernel)(Matrix, Matrix, Matrix),
const Matrix &A, const Matrix &B, Matrix &C,
dim3 gridDim, dim3 blockDim)
{
// Load matrices to device memory
Matrix d_A, d_B, d_C;
size_t size_A = A.width * A.height * sizeof(float);
size_t size_B = B.width * B.height * sizeof(float);
size_t size_C = C.width * C.height * sizeof(float);
d_A.width = A.width; d_A.height = A.height;
d_B.width = B.width; d_B.height = B.height;
d_C.width = C.width; d_C.height = C.height;
// Allocate device memory
CUDA_CHECK_ERROR(cudaMalloc(&d_A.elements, size_A));
CUDA_CHECK_ERROR(cudaMalloc(&d_B.elements, size_B));
CUDA_CHECK_ERROR(cudaMalloc(&d_C.elements, size_C));
// Copy A, B to device memory
CUDA_CHECK_ERROR(cudaMemcpy(d_A.elements, A.elements, size_A, cudaMemcpyHostToDevice));
CUDA_CHECK_ERROR(cudaMemcpy(d_B.elements, B.elements, size_B, cudaMemcpyHostToDevice));
auto start = std::chrono::high_resolution_clock::now();
// Launch kernel
kernel<<<gridDim, blockDim>>>(d_A, d_B, d_C);
// Synchronize device memory
CUDA_CHECK_ERROR(cudaDeviceSynchronize());
auto end = std::chrono::high_resolution_clock::now();
std::chrono::duration<float> duration = end - start;
std::cout << "Kernel execution time: " << duration.count() * 1000.0f << " ms" << std::endl;
// Copy C from device memory to host memory
CUDA_CHECK_ERROR(cudaMemcpy(C.elements, d_C.elements, size_C, cudaMemcpyDeviceToHost));
// Free device memory
CUDA_CHECK_ERROR(cudaFree(d_A.elements));
CUDA_CHECK_ERROR(cudaFree(d_B.elements));
CUDA_CHECK_ERROR(cudaFree(d_C.elements));
}And, we call runKernel() function in above defined main() function.
CUDA Shared Memory Kernel
The previous CUDA kernel uses DRAM, but we can optimize performance by leveraging the GPU’s shared memory. Shared memory is faster but has limited capacity, so we cannot load entire matrices at once. Instead, we divide the matrices into smaller sub-matrices, or tiles, that fit into shared memory.
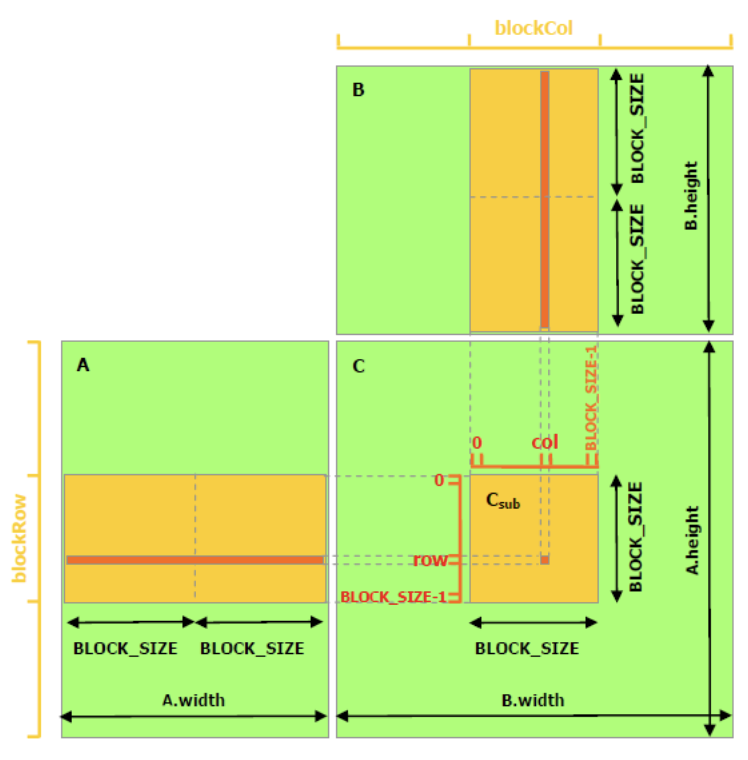
Shared memory is allocated per thread block, allowing threads within the same block to communicate efficiently. Each thread block is responsible for computing one square sub-matrix \(C_{sub}\) of C by loading tiles of input matrices A and B from global memory to shared memory. Each thread within the block computes a single element of \(C_{sub}\) by iterating over the corresponding elements in the shared memory tiles, accumulating the results of the products. Finally, each thread writes its computed value to the appropriate position in global memory.
#define TILE_SIZE 16
// Kernel for matrix multiplication using tiling and shared memory
__global__ void matMulSharedMemoryKernel(Matrix A, Matrix B, Matrix C)
{
// Shared memory for tiles of A and B
__shared__ float shared_A[TILE_SIZE][TILE_SIZE];
__shared__ float shared_B[TILE_SIZE][TILE_SIZE];
// Calculate the global row and column index of the element
int globalRow = blockIdx.y * blockDim.y + threadIdx.y;
int globalCol = blockIdx.x * blockDim.x + threadIdx.x;
float Cvalue = 0.0f;
// Thread row and column within Csub
int row = threadIdx.y;
int col = threadIdx.x;
// Loop over the tiles of the input matrices
// A.width/TILE_SIZE and B.height/TILE_SIZE; take care of the last tile
for (int m = 0; m < (A.width + TILE_SIZE - 1) / TILE_SIZE; ++m)
{
// Load elements of A into shared memory
// if shared memory defined using 1d array, we'd have used shared_A[row * TILE_SIZE + col]
if (row < A.height && (m * TILE_SIZE + col) < A.width)
{
shared_A[row][col] = A.elements[globalRow * A.width + m * TILE_SIZE + col];
} else
{
// When matrix dimensions are not exact multiples of the tile size,
// some threads in the last blocks might access elements outside
// the matrix boundaries. By setting out-of-bounds elements to zero,
// we ensure that these threads do not contribute invalid values to final result.
// e.g. Matrix A = [100x100] and TILE_SIZE = 16
shared_A[row][col] = 0.0f;
}
// Load elements of B into shared memory
if (col < B.width && (m * TILE_SIZE + row) < B.height)
{
shared_B[row][col] = B.elements[(m * TILE_SIZE + row) * B.width + globalCol];
} else
{
shared_B[row][col] = 0.0f;
}
// Synchronize to ensure all threads have loaded their elements
__syncthreads();
// Compute the partial result
for (int k = 0; k < TILE_SIZE; ++k)
Cvalue += shared_A[row][k] * shared_B[k][col];
// Synchronize to ensure all threads have completed the computation
__syncthreads();
}
// Write the result to global memory
if (globalRow < C.height && globalCol < C.width)
C.elements[globalRow * C.width + globalCol] = Cvalue;
}We can call our kernel as follows:
dim3 blockDim(TILE_SIZE, TILE_SIZE);
dim3 gridDim((C.width + TILE_SIZE - 1) / TILE_SIZE, (C.height + TILE_SIZE - 1) / TILE_SIZE);
runKernel(matMulSharedMemoryKernel, A, B, C, gridDim, blockDim);CUDA Matrix Multiplication Comparison
The kernel execution time of above kernels on Tesla T4 on google colab is as follows.
| Method | Execution Time (ms) |
|---|---|
| C++ CPU matrix multiplication | 8554.51 |
| Naive CUDA kernel | 7.08397 |
| Shared memory CUDA kernel | 4.42471 |
The CUDA parallelism significantly improves the CPU computation time. The shared memory kernel achieves the fastest execution time.
The full code is availble at https://github.com/kHarshit/cuda-programming
Further Optimization
There are other ways to optimize the CUDA matrix multplication kernel further, such as:
- Using Register Blocking: This technique involves utilizing the register file to hold smaller sub-blocks of the matrices, reducing the number of accesses to shared memory.
- Loop Unrolling: By unrolling loops, you can decrease the overhead of loop control instructions and increase the efficiency of the computation.
- Occupancy Optimization: Tuning the number of threads per block and the size of the blocks to achieve the highest possible occupancy on the GPU.
- Prefetching: Loading data into shared memory or registers ahead of time to hide memory latency.
- Asynchronous Memory Operations: Using CUDA streams and
cudaMemcpyAsyncto overlap computation and data transfer, further reducing idle times. - Low Precision: Using half-precision (FP16) or mixed-precision (FP16/FP32) arithmetic can improve performance on supported GPUs.
By combining these advanced optimization techniques with shared memory, you can achieve even greater performance gains for matrix multiplication on CUDA-enabled GPUs.
References