First, make sure you read the first part of this post, Generative models and Generative Adversarial Networks. This post is its continuation.

Generative Adversarial Networks (GANs) are used for generation of new data i.e. images. It consists of two distinct models, a generator and a discriminator, competing with each other.

DCGAN

A Deep Convolutional GAN or DCGAN is a direct extension of the GAN, except that it explicitly uses convolutional and transpose-convolutional layers in the discriminator and generator, respectively. The discriminator is made up of strided convolution layers, batch norm layers, and LeakyReLU activations without max-pooling layers i.e. convolution > batch norm > leaky ReLU.

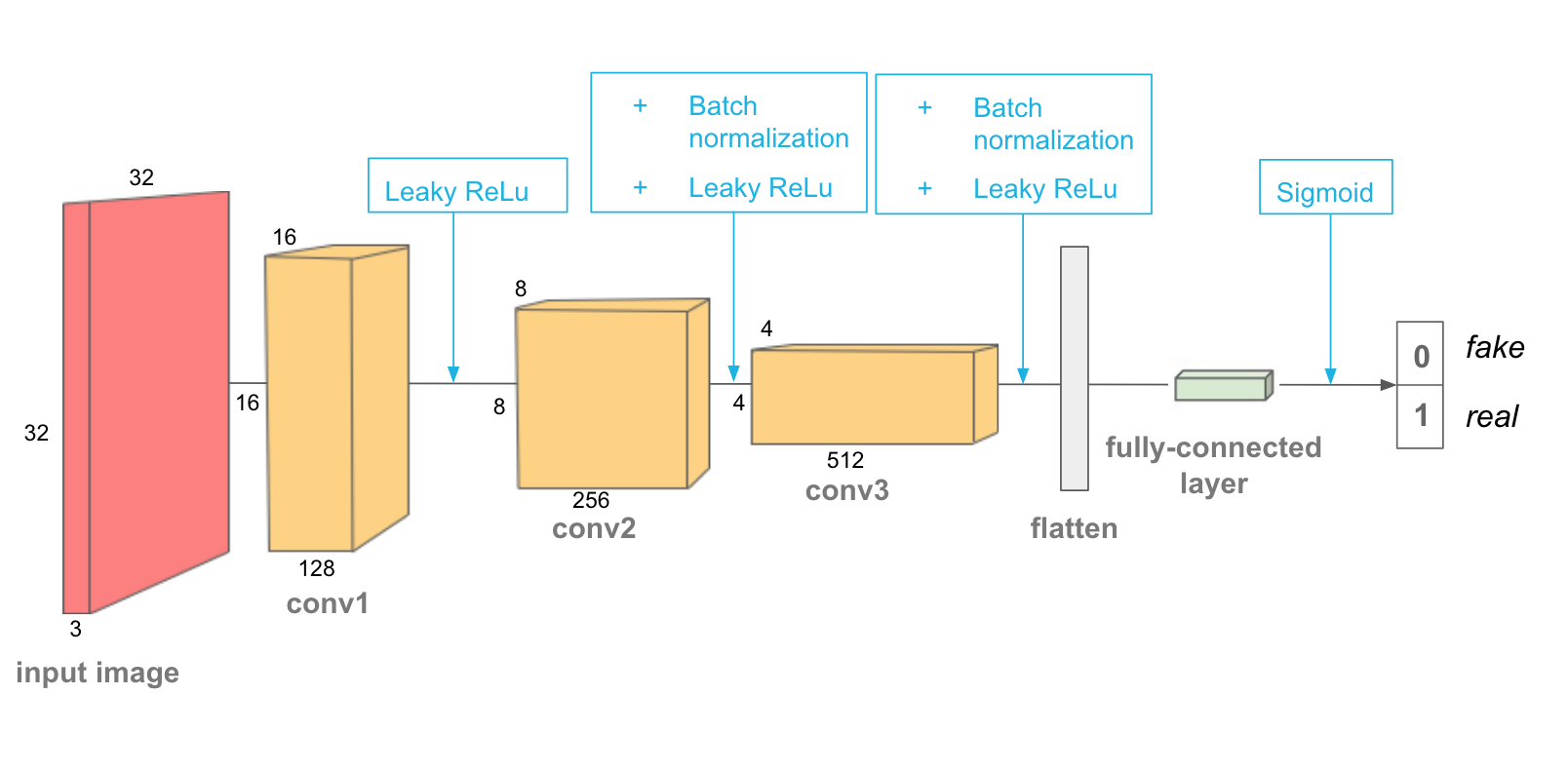
A helper function consisting of convolutional and batch norm layer can be created in PyTorch for ease as follows.

import torch.nn as nn
import torch.nn.functional as F

def conv(in_channels, out_channels, kernel_size, stride=2, padding=1, batch_norm=True):
    """Creates a helper layer: convolutional layer, with optional batch normalization
    """
    layers = []
    conv_layer = nn.Conv2d(in_channels, out_channels, 
                           kernel_size, stride, padding, bias=False)
    
    # append conv layer
    layers.append(conv_layer)

    if batch_norm:
        # append batchnorm layer
        layers.append(nn.BatchNorm2d(out_channels))
     
    # using Sequential container
    return nn.Sequential(*layers)

The generator is comprised of transpose-convolutional layers, batch norm layers, and ReLU activations i.e. transpose convolution > batch norm > ReLU.

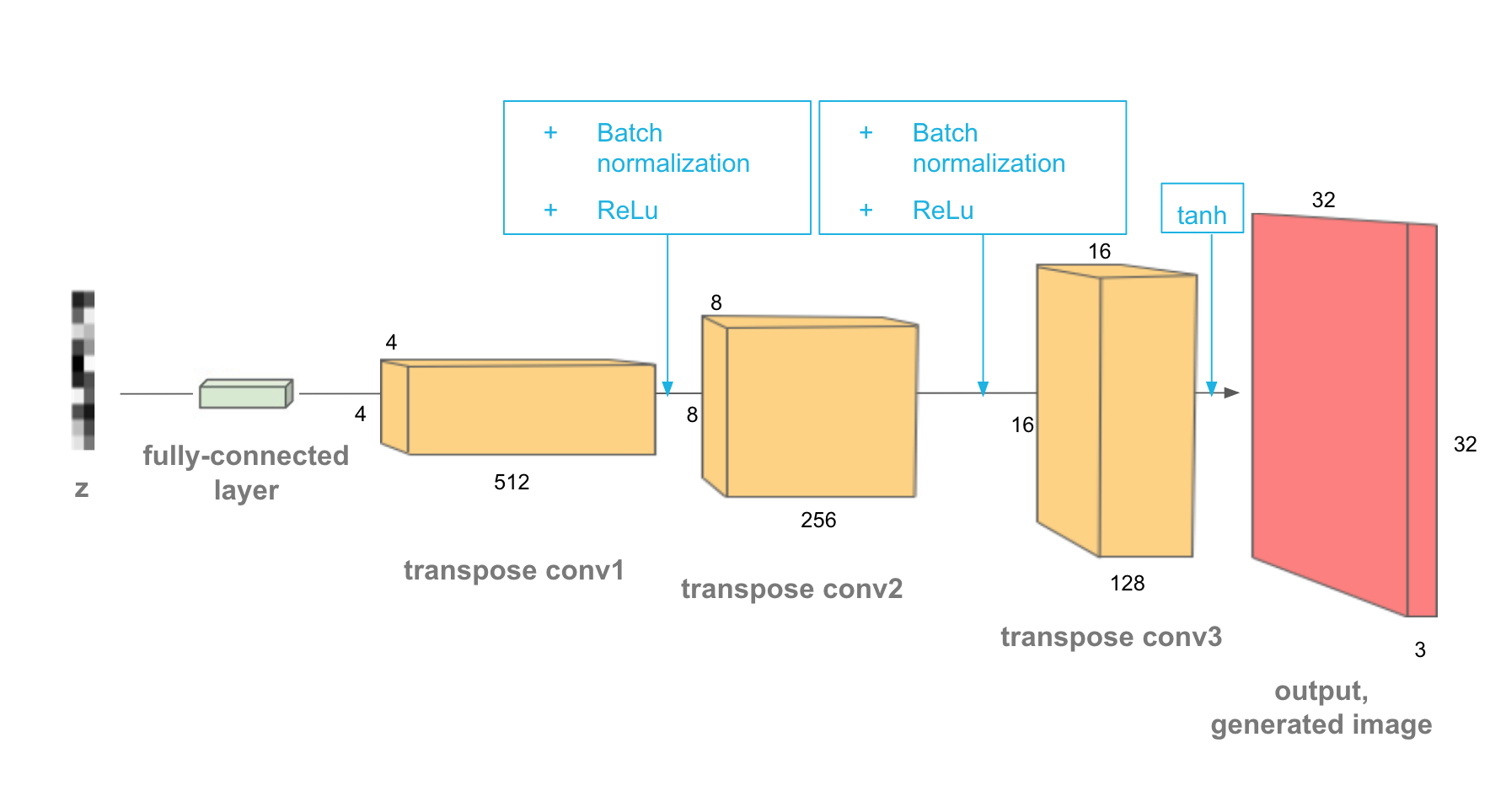
The training is same as in case of GAN.

Note: The complete DCGAN implementation on face generation is available at kHarshit/pytorch-projects.

Pix2pix

Pix2pix uses a conditional generative adversarial network (cGAN) to learn a mapping from an input image to an output image. It’s used for image-to-image translation.

To train the discriminator, first the generator generates an output image. The discriminator looks at the input/target pair and the input/output pair and produces its guess about how realistic they look. The weights of the discriminator are then adjusted based on the classification error of the input/output pair and the input/target pair. The generator’s weights are then adjusted based on the output of the discriminator as well as the difference between the output and target image.

The generator consists of Encoder that converts the input image into a smaller feature representation, and Decoder, which looks like a typical generator, a series of transpose-convolution layers that reverse the actions of encoder layers. The discriminator, instead of identifying a single image as real or fake, will look at pairs of images (input image and unknown image that is either targete image or generated image), and output a label for pair as real or fake. The loss function is (compare with this):

The problem with pix2pix is training because the two image spaces are needed to be pre-formatted into a single X/Y image that held both tightly-correlated images.

CycleGAN

CycleGAN is also used for Image-to-Image translation. The objective of CycleGAN is to train generators that learn to transform an image from domain 𝑋 into an image that looks like it belongs to domain 𝑌 (and vice versa). CycleGAN uses an unsupervised approach to learn mapping from one image domain to another i.e. the training images don’t have labels. The direct correspondence between individual images is not required in domains.

A CycleGAN is made of two discriminator, and two generator networks. The discriminators, \(D_Y\) and \(D_X\), which are convolutional neural networks that classify an input image as real or fake, learn the mappings \(G: X \rightarrow Y\) and \(F: Y \rightarrow X\) respectively. \(D_Y\) encourages \(G\) to translate \(X\) into outputs indistinguishable from domain \(Y\), and vice versa for \(D_X\) and \(F\).

The generators, \(G_XtoY\) and \(G_YtoX\), are made of an encoder, a conv net that is responsible for turning an image into a smaller feature representation, and a decoder, a transpose-conv net that is responsible for turning that representation into an transformed image.

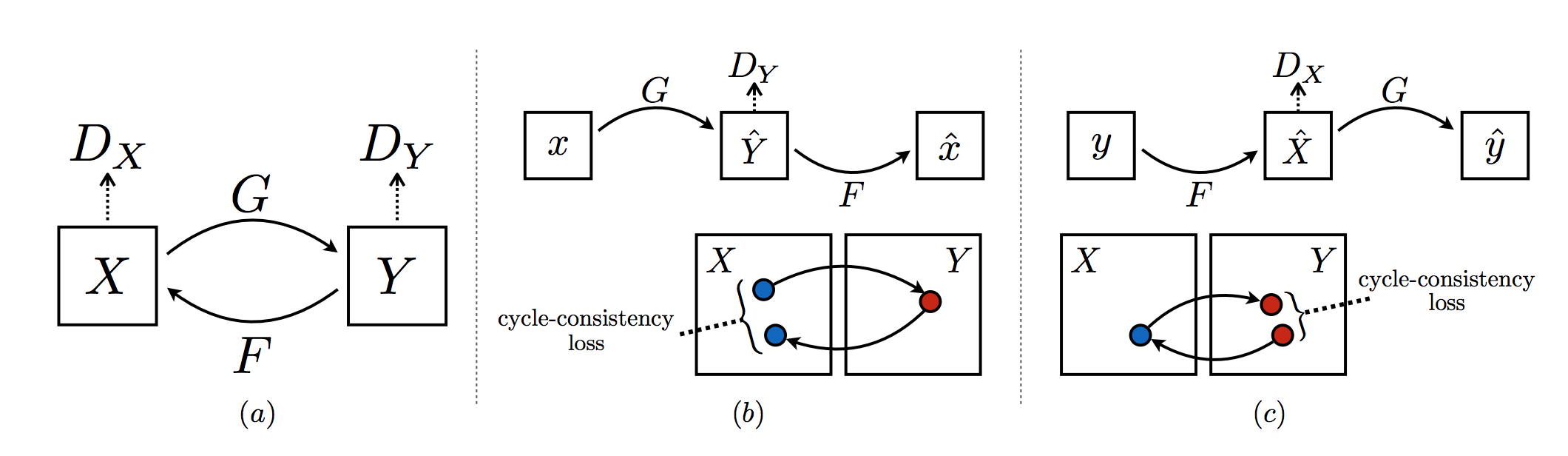
For discriminator, least squares GAN or LSGAN is used as loss function to overcome the problem of vanishing gradient while using cross-entropy loss i.e. the discriminator losses will be mean squared errors between the output of the discriminator, given an image, and the target value, 0 or 1, depending on whether it should classify that image as fake or real.

In addition to adversarial losses, two cycle consistency losses, Forward cycle-consistency loss and backward cycle-consistency loss, are also used to ensure if we translate from one domain to the other and back again we should arrive at where we started. This loss is measures of how good a reconstructed image is, when compared to an original image. Thus, the total generator loss will be the sum of the generator losses and the forward and backward cycle consistency losses.

Further Readings:

1. DCGAN paper
2. DCGAN tutorial - PyTorch official tutorials
3. Pix2pix homepage
4. CycleGAN paper
5. CycleGAN and pix2pix in PyTorch