The Bayesian Thinking - II
Friday, June 15, 20183 mins read
Statistics is the study of uncertainity. One way to deal with uncertainity is by probabilities.
Read the first post The Bayesian Thinking - I.
Models of probability
- Classical: In classical framework, outcomes that are equally likely have equal probabilities e.g. in case of rolling of dice, there are six equally likely outcomes, so
P[rolling a four] = 1/6. - Frequentist: The Frequentist definition of probability requires to have an infinite hypothetical sequence of events, then look at relevant frequency e.g. in case of rolling of dice, if the die is rolled an infinite number of times, then one sixth of the time, we’ll get a four hence,
P[rolling a four] = 1/6. - Bayesian: The Bayesian perspective of probability is a personal perspective. For example, to check if the die is fair, if you have different information from someone else then your
P[die is fair]will be different than that person’s. It interprets probability as a measure of belief that an individual may possess about the occurrence of an event i.e. you may have prior belief about an event, but those beliefs are likely to change in case of new evidence. The Bayesian probablity provide tools to update subjective beliefs in light of new evidence (data).
Bayesian Statistics [Contd…]
- Principle 1: Use prior knowledge
- Principle 2: Choose answer that explains the observation the most
- Principle 3: Avoid making extra assumptions
Let’s take an example of finding probability of coin being fair. Let’s say an individual has a prior belief that the coin is fair. If after a number of tosses, say 500, the coin comes up head 400 times then the individual’s belief will be updated to coin is unfair.
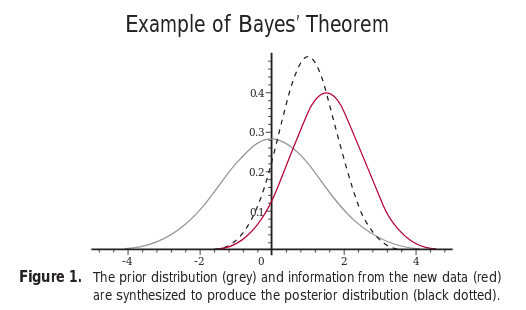
Thus in Bayesian interpretation, the probability is a summary of an individual’s opinion. The different individuals may have different opinion (prior belief), as they might have different data and ways of interpreting it. However, as both of theses individuals get new information (data), their potentially differing beliefs leads to the same posterior belief.
Frequentist vs Bayesian
According to the Frequentist theory, only repeatable events have probabilities. In the Bayesian framework, probability simply describes uncertainty.
Frequentist notion is objective while the Bayesian one is subjective.
In frequentist statistics, parameters (\(\theta\)) are fixed as they are specific to the problem, and are not subject to random variablility so probability statements about them are not meaningful while data (\(X\)) is random. On the other hand, in Bayesian statistics, parameters (\(\theta\)) are random (unknown) thus direct probability statements about parameters are made and data (X) is fixed.
e.g. Consider the following statements:
- Statement 1: We reject null hypothesis at the 5% level of significance.
- Statement 2: The probability that this hypothesis is true is 0.05.
Statement 1 is a frequentist one. It means that if we were to repeat the analysis many times, using new data each time, then in 5% of samples where the null hypothesis is true it will be (falsely) rejected (but nothing is stated about this sample). Statement 2 is Bayesian. It applies on the basis of this sample (as a degree of belief).
The Bayesian methods work for any number of data points (i.e. for any \(\mid X\mid\)), while frequentists method work only when number of data points is greater than number of parameters (i.e. \(\mid X\mid > \theta\)).
The frequentist train their model using maximum liklihood principle (\(\hat\theta = max(P[X \mid \theta]))\) i.e. they try to find the parameter that maximizes the liklihood, the probability of data given parameters. However, the Bayesian will try to compute the posterior probability, the probability of parameters given data, using Bayes theorem. \(P[\theta \mid X] = \frac{P[X\mid\theta].P(\theta)}{P(X)}\)
[Read the last part: The Bayesian Thinking - III]
References: