Attention is the technique through which the model focuses itself on a certain region of the image or on certain words in a sentence just like the same way the humans do. For example, when looking at an image, humans shifts their attention to different parts of the image one at a time rather than focusing on all parts in equal amount at the same time.

Encoder-Decoder architecture

A Recurrent Neural Network (RNN) can be used to map a varied-length input sequence to the varied-length output sequence e.g. machine translation. The simplest sequence-to-sequence architecture that makes it possible consists of two models, Encoder, and Decoder. In Encoder-Decoder architecture, the idea is to learn a fixed-size context vector that contains the essential information of the inputs.

• The Encoder processes the input sequence \((x_1, x_2, x_3, ..., x_n)\) and gives a context vector, C that summarizes the input sequence.
• The Decoder uses C to generate the output sequence \((y_1, y_2, y_3, ..., y_m)\), where n and m may not be equal.

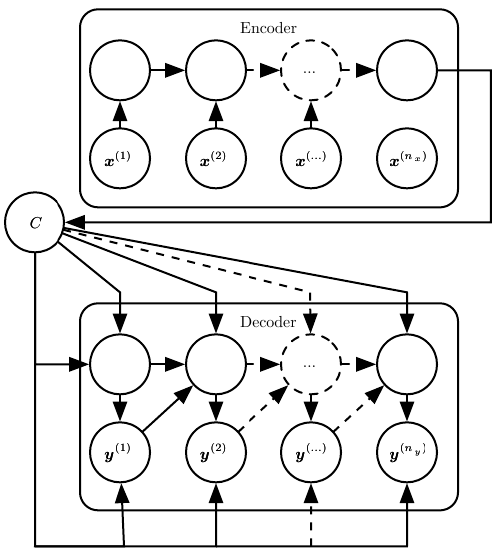
The final hidden state of the hidden state of encoder RNN is used to compute C, which is further provided as an input to the decoder.

The problem with encoder-decoder approach is that all the input information needs to be compressed in a fixed length context vector, C. It makes it difficult for the network to cope up with large amount of input information (e.g. in text, large sentences) and produce good results with only that context vector. With attention mechanism, the encoder RNN instead of producing a single context vector to summarize the input image or sequence, produces a grid of vectors. That is, attention makes C a variable-length sequence rather than a fixed-size vector.

Every step in the decoder (only) requires calculation of attention vector in seq2seq model. The Attention decoder uses a scoring function to score each hidden state. These scores when fed into a softmax function gives the weight of each vector in the attention vector. Now, these weights are multiplied by corresponding hidden state vector, whose sum gives the attention context vector. The decoder at each step looks at input sequence as well as attention context vector, which focuses its attention at appropriate place in input sequence, and produces the hidden state.

The important part is that each decoder output \(y_t\) now depends on a weighted combination of all the input states, not just the last state.

The decoder has hidden state \(s_t=f(s_{t−1},y_{t−1},c_t)\) for the output word at position t, where t=1,…,m, where the context vector \(c_t\) is a sum of hidden states of the input sequence, weighted by alignment scores

The alignment model assigns a score \(α_{t,i}\) to the pair of input at position i and output at position t, \((y_t,x_i)\), based on how well they match. The set of scores \(\{\alpha_{t, i}\}\) are weights defining how much of each source hidden state should be considered for each output.

Additive and Multiplicative Attention

The Additive (Bahdanau) attention differs from Multiplicative (Luong) attention in the way scoring function is calculated. The additive attention uses additive scoring function while multiplicative attention uses three scoring functions namely dot, general and concat.

Further Readings:

1. Attention and Memory in Deep Learning and NLP
2. How Does Attention Work in Encoder-Decoder Recurrent Neural Networks
3. Attention? Attention!
4. PyTorch Deep Learning Nanodegree - Udacity (also image source)