Loss functions
Friday, August 24, 20182 mins read
In machine learning, the difference between the predicted output and the actual output is used to tune the parameters of the algorithm. This error in prediction, so called loss, is a crucial part of designing a good model as it evaluates the performance of our model. For accurate predictions, one needs to minimize this loss. In neural networks, it is done using the gradient descent. There are many types loss functions. Some of them are:
L2 loss (Mean-squared error)
Mean squared error is the most common used loss function for regression loss. It minimizes the squared difference between the predicted value and the actual value. The residual sum of squares is defined as:
\[RSS = \sum_{i=1}^n(y_{i} - \hat{y_i})^2\]import numpy as np
def l2_loss(yhat, y):
return np.sum((yhat - y)**2))L1 loss (Mean-absolute error)
L1 loss minimized the sum of absolute error between the predicted value and the actual value.
\[L(y, \hat{y}) = \sum_{i=1}^n \left| y_{i} - \hat{y_i} \right|\]def l1_loss(yhat, y):
return np.sum(np.absolute(yhat - y))Note: L1 and L2 are also used in regularization. Don’t get confused.
Hinge loss
The hinge loss is used for classification problems e.g. in case of suppport vector machines. It is defined as:
\[L(y, \hat{y}) = max(0, 1-\hat{y} * y)\]def hinge(yhat, y):
return np.max(0, 1 - yhat * y)Cross-entropy (log loss)
The cross-entropy loss is also used in case of classification problems for estimating the accuracy of model whose output is a probability, p, which lies between 0 and 1. In case of binary classification, it can be written as:
For multi-class classification problems, it is:
\[L(y) = -\sum_{c=1}^n y_{o,c}\log(p_{o,c})\]Here, y is a binary indicator (0 or 1) if class label c is the correct classification for observation o and p is predicted probability observation s.t. o is of class c.
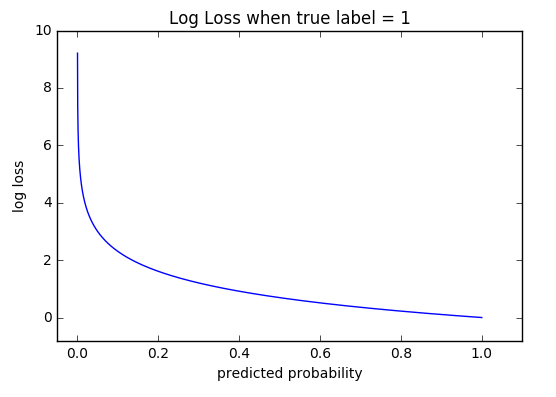
def cross_entropy(y, p):
return -np.sum(np.multiply(y, np.log(p)) + np.multiply((1-y), np.log(1-p)))For a detailed example using log loss, check logistic regression implementation on GitHub: kHarshit/ML-py.
Conclusion
The choice of loss function depends on the class of problem (regression / classification) as well as is sometimes specific to the problem.
References: