Methods of Hyperparameter optimization
Friday, August 3, 20183 mins read
The parameters, called hyperparameters, that define the performance of the machine learning algorithm (model), depends on the problem we are trying to solve. Thus, they need to be configured accordingly. This process of finding the best set of parameters is called hyperparameter optimization. For example, in support vector machines (SVM), regularization constant C, kernel coefficient γ need to be optimized. The tuning of optimal hyperparameters can be done in a number of ways.
Grid search
The grid search is an exhaustive search through a set of manually specified set of values of hyperparameters. It means you have a set of models (which differ from each other in their parameter values, which lie on a grid). What you do is you then train each of the models and evaluate it using cross-validation. You then select the one that performed best.
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
iris = load_iris()
svc = SVC()
# grid search on kernel and C hyperparameters
parameters = {'kernel':('linear', 'rbf'), 'C':[1, 10]}
clf = GridSearchCV(svc, param_grid=parameters)
clf.fit(iris.data, iris.target)
>>> print('Grid best parameters (max accuracy): ', clf.best_params_)
Grid best parameters (max accuracy): {'C': 1, 'kernel': 'linear'}
>>> print('Grid best score (accuracy): ', clf.best_score_)
Grid best score (accuracy): 0.98Random search
Random search searches the grid space randomly instead of doing exhaustive search i.e. it tries randomly selected combinations of parameters. In case of deep learning algorithms, it outperforms grid search.
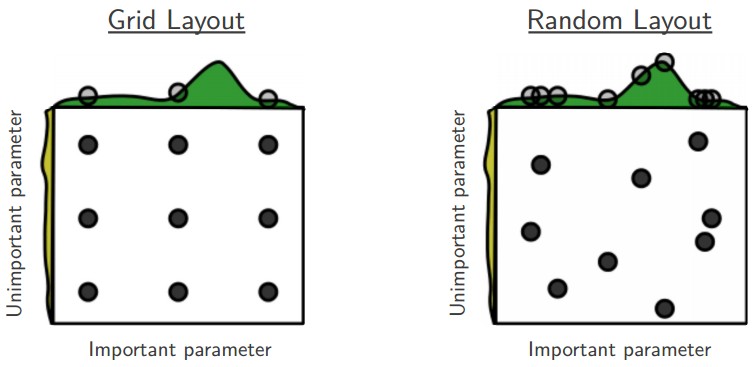
Often some of the hyperparameters matter much more than others. Performing random search rather than grid search allows much more precise discovery of good values for the important ones.
from sklearn.model_selection import RandomizedSearchCV
random_search = RandomizedSearchCV(clf, param_distributions=parameters,
n_iter=10)Bayesian optimization
The Bayesian optimization builds a probabilistic model to map hyperparmeters to the objective fuction. It computes the posterior predictive distribution. It iteratively evaluates a promising hyperparameter configuration, and updates the priors based on the data, to form the posterior distribution of the objective function and tries to find the location of the optimum. The Bayesian optmization balances exploration and exploitation so is suited for functions that are expensive to evaluate.
Gradient-based optimization
It is specially used in case of neural networks. It computes the gradient with respect to hyperparameters and optimize them using the gradient descent algorithm.
Evolutionary optimization
This methodology uses evolutionary algorithms to search the hyperparameter space.
References: