Don't use sigmoid: Neural Nets
Friday, April 20, 20182 mins read
In neural networks, activation functions are used to introduce non-linearity in the model. There are several activation functions to choose from. Traditionally, people have been using sigmoid as the activation function. But, you shouldn’t use it. Why? Let’s see.
Sigmoid
It is defined as
\[\sigma(x) = \frac{1}{(1 + e^{-x})}\]It returns a value between 0 and 1. The two major problems with sigmoid activation functions are:
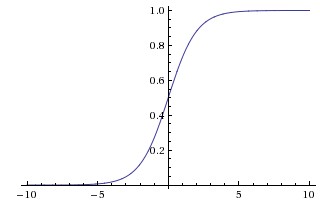
- Sigmoid saturate and kill gradients: The output of sigmoid saturates (i.e. the curve becomes parallel to x-axis) for a large positive or large negative number. Thus, the gradient at these regions is almost zero. During backpropagation, this local gradient is multiplied with the gradient of this gates’ output. Thus, if the local gradient is very small, it’ll kill the the gradient and the network will not learn. This problem of vanishing gradient is solved by ReLU.
- Not zero-centered: Sigmoid outputs are not zero-centered, which is undesirable because it can indirectly introduce undesirable zig-zagging dynamics in the gradient updates for the weights.
What are the options?
There are other activation functions such as
Tanh: It gives a value in range of [-1, 1] for a real number. But, as in sigmoid, its output saturate but are zero-centered.
ReLU: Rectified Linear Unit is another popular choice. It is defined as
\[f(x) = max(0, x)\]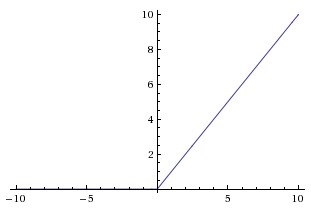
It solves the problem of saturation (though only in the positive region). In the negative region, the gradient is zero, hence again the weights of the network do not update. Also, ReLU units can die during training e.g. a large gradient flowing through a ReLU neuron could cause the weights to update in such a way that the neuron will never activate on any datapoint again. Thus, if learning rate is set too high, as much as 40% of your network can be dead (i.e. neurons that never activate across the entire training dataset). However, this problem can be solved with the proper setting of the learning rate.
Leaky ReLU: Leaky ReLU are an attempt to solve the dying ReLU problem. It has a small negative slop when x < 0 i.e.
\[f(x) = 1(x < 0) (\alpha x) + 1(x>=0) (x)\]Note that it doesn’t always guarantee success.
Conclusion
What activation function one should use?
Use the ReLU activation. But, set the learning rates carefully to avoid the dying ReLU problem. Try Leaky ReLU also. But, don’t use sigmoid.
References: