Overfitting and Underfitting
Friday, October 13, 20172 mins read
In machine learning, sometimes the prediction of our model may not be satisfactory. Although there may be many reasons for that, often it is due to either overfitting or underfitting of the model.
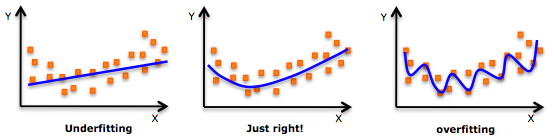
If we have too many features, the machine learning model may fit the training data very well, but fail to generalize to the test data. It is because our model is too complex for the amount of training data available thus not generalize to new examples. This problem is known as overfitting.
Think of overfitting as memorizing as opposed to learning.
On the other hand, underfitting occurs when our model is too simple to capture the underlying trend of the data thus doesn’t even perform well on the training data and not likely to generalize well on the testing data as well. For example, when fitting a linear model to non-linear data. Such a model would have poor predictive performance.
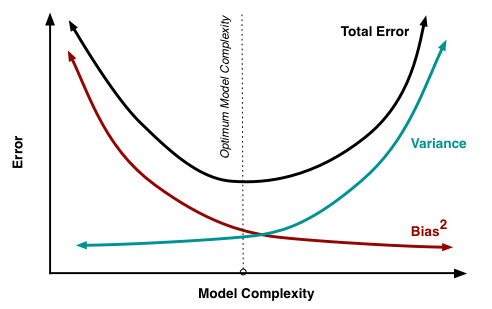
Bias-Variance tradeoff
The bias is the difference between the model’s predictions and the true values. High bias can cause the model to underfit.
The variance is the model’s sensitivity to small fluctuations in the training set. High variance can cause the model to overfit.
To get good predictions, you’ll need to find a balance of bias and variance the minimizes the total error.
How to solve the problem of overfitting?
In order to address the problem of overfitting, there are a number of techniques as:
- Reduce the number of features.
- Regularization: Add the penalty parameter to the cost function so we penalize the model by increasing the penalty for overfitted model.
- Cross-validation: It involves randomly dividing the training data into k groups, or folds, of approx. equal sizes. The first fold treated as validation set, and the model is fit on the remaining k - 1 folds. This procedure is repeated k times; each time, a different group of observations is treated as a validation set. The k results from the folds can then be averaged to produce a single estimation.
References:
Image source: http://scott.fortmann-roe.com/docs/BiasVariance.html