Weight initialization in neural nets
Friday, February 8, 20192 mins read
In deep learning, the goal is to find the optimum weights of the model to get the desired output. In transfer learning, the network is initialized using the best pre-trained weights. The question is how do you initialize the weights for a non-pretrained model?
Training algorithms for deep learning models are usually iterative in nature and thus require the user to specify some initial point from which to begin the iterations. Moreover, training deep models is a sufficiently difficult task that most algorithms are strongly affected by the choice of initialization. — Deep Learning (book)
There are numerous weight initialization methods:
All 0s or All 1s
One of the ways is to initialize all weights to 0s. As all the weights are same, the activations in all hidden units are also the same. This makes the gradient w.r.t to each weight be same. Thus, the problem arises as to which weight the network should update and by how much i.e. backpropagation finds it difficult to minimize the loss. The same problem occurs if all weights are initialized as 1s.
In PyTorch, nn.init is used to initialize weights of layers e.g. to change Linear layers’s initialization method:
def init_weights(m, constant_weight):
"""initialize weight of Linear layer as constant_weight"""
if type(m) == nn.Linear:
nn.init.constant_(m.weight, constant_weight)
m.bias.data.fill_(0)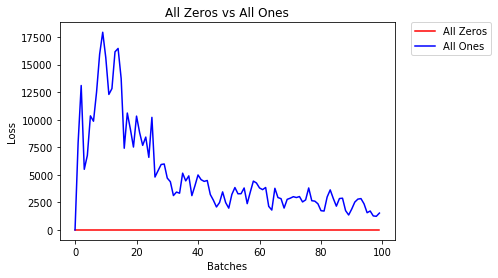
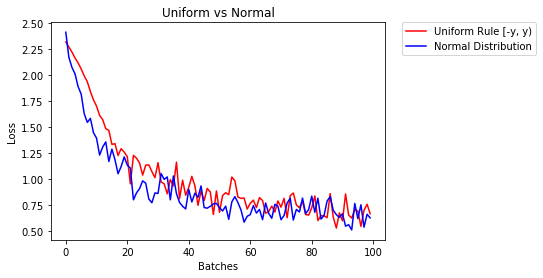
Uniform distribution
The other way is to initialize weights randomly from a uniform distribution. Every number in uniform distribution has equal probability to be picked.
In PyTorch, the Linear layer is initialized with He uniform initialization, nn.init.kaiming_uniform_, by default.
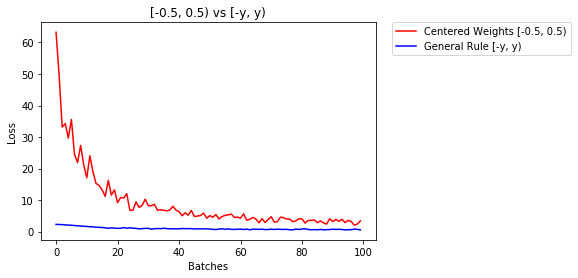
General rule
Choosing high values of weights is not the best for the model as it brings problems of exploding and vanishing gradients. The general way to initialize weights is to select small random values, which are close to 0.
Good practice is to start your weights in the range of \([-y, y]\) where \(y=1/\sqrt{n}\)
(\(n\) is the number of inputs to a given neuron).
Normal distribution
Another way is to initialize weights randomly from a normal distribution. As most values are concentrated towards the mean, most of the random values selected have higher probability to be closer to mean (say \(\mu=0\)).
There are many other ways for weight initialization such as Xavier initialization. It’s an active area of research.
References:
- PyTorch Deep Learning Nanodegree - Udacity
- PyTorch’s nn.init
- PyTorch Linear layer source code
- (He initialization) Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
- (Xavier initialization) Understanding the difficulty of training deep feedforward neural networks