A visual introduction to eigenvectors and eigenvalues
Friday, May 11, 20182 mins read
The word eigen, having a German origin, means characteristics. The eigenvalues and eigenvectors give the characteristic, but of what? Let’s understand it through a geometric example.
The linear transformations such as scaling, rotation, and shearing can be expressed using matrices. For example, by applying a vertical scaling of +2 to every vector of a square, will transform the square into a rectangle. In the same way, by applying a horizontal shear to the square, it becomes a parallelogram.
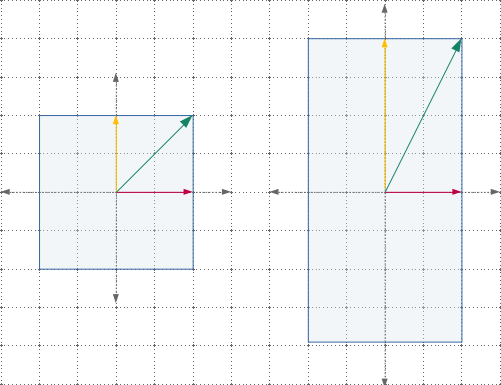
Note that during these transformations, some of the vectors remain on the same line (span) as they were earlier. As shown in the figure,
- The horizontal vector remains unchanged (same direction, same length).
- The vertical vector has same direction, but doubled in length.
- The diagonal vector has changed its angle (direction) as well as length.
Note that, in the above figure, after vertical scaling of +2, every vector’s (except horizontal and vertical ones) direction has changed. These two vectors are special and are the characteristic of this particular transform. Hence, these are called eigenvectors.
An eigenvector is a vector, which after applying the linear transformation, stays in the same span i.e. changes by only a scalar factor.
The eigenvalue is how much the eigenvectors are transformed (stretched or diminished).
- The horizontal vector’s length remains same, thus have an eigenvalue of +1.
- The vertical vectors’ length doubled, thus have an eigenvalue of +2.
Examples
In the same way, the horizontal shear transformation to square gives only one eigenvector (horizontal one) having an eigenvalue of +1.
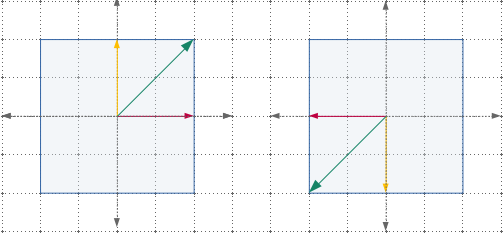
In 180 degree rotation of square, all vectors are still laying on the same span, but their direction is reversed. Hence, all vectors are eigenvectors, having an eigenvalue of -1.
In case of 3d rotation transformation of cube, the eigenvector gives the axis of rotation.
Mathematics
Suppose we have a transformation matrix A and we apply this transformation to vector x. This will be equivalent to stretching (or diminshing) the vector x by a scalar factor λ.
where I is the identity matrix.

The above euqation has a non-zero solution iff the determinant of the matrix (A − λI) is zero i.e.
Evaluating this determinant gives the characteristic polynomial i.e.
\[\text{if } A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\] \[\begin{vmatrix} \begin{bmatrix} a & b \\ c & d \end{bmatrix} - \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \end{bmatrix} \end{vmatrix} = 0\] \[\lambda ^ 2 - (a+d)\lambda + ad - bc = 0\]The solution of this equation gives the eigvenvalues. Put these eigenvalues in the original expression to get their corresponding eigenvectors.
References: