Introduction to Automatic Speech Recognition
Friday, April 19, 20193 mins read
The Automatic Speech Recognition (ASR) systems are widely used nowadays. Some of the most notable uses include Siri, Alexa Google Assistant, Cortana, etc. Let’s understand the fundamentals of ASR.
Introduction
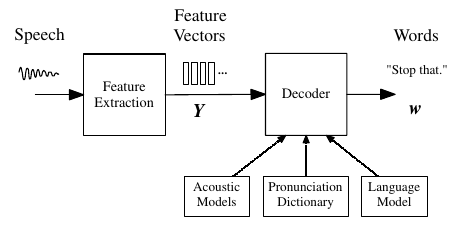
Hidden Markov Models (HMM) can be used for ASR. The HMM based recognizer consists of two key components, feature extractor, and decoder.
- First, in feature extraction, the input audio signal is converted into a sequence of fixed size acoustic vectors \(Y = y_1, \dots, y_t\).
- The decoder then finds the sequence of words \(w = w_1, \dots, w_l\) corresponding to
Yi.e. the decoder calculates
However, it’s difficult to model \(P(w \mid Y)\), the Bayes rule is used to transform the above equation into an equivalent one as follow:
\[\hat{\boldsymbol{w}}=\underset{\boldsymbol{w}}{\arg \max }\{p(\boldsymbol{Y} | \boldsymbol{w}) P(\boldsymbol{w})\}\]The model that determines \(P(Y \mid w)\) is called acoustic model and the one that models \(P(w)\) is called a language model.
Feature extraction
The feature extraction phase deals with the representation of input signal. The Mel-frequency cepstral coefficients (MFCC) or Linear Predictive Coding (LPC) vectors can be used as acoustic vectors, Y.
Acoustic model
A HMM is used to model \(P(Y \mid w)\). The extracted feature vectors from the unknown input audio signal is scored against acoustic model, the output of the model with max score is choosen as the recognized word. The Gaussian Mixture Model (GMM) can be used as the acoustic model.
The basic unit of sound that acoustic model represents is called phoneme e.g. the word “bat” has three phonemes \(/ \mathrm{b} / / \mathrm{ae} / / \mathrm{t} /\). The concatenation of these phonemes, called pronunciation, can be used to represent any word in the English language. Thus, in order to recognize a given word, the task is to extract phonemes from input signal.
Remember that HMM is a finite state machine that changes its state every time step. In HMM based speech recognition, it is assumed that the sequence of observed speech vectors corresponding to each word is generated by a Markov model. Each phoneme (basic unit) is assigned a unique HMM, with transition probability parameters \(a_{ij}\) and output observation distributions \(b()\).
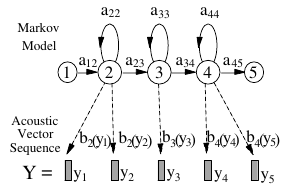
For a isolated (single) word recognition, the whole process can be described as follows:
Each word in the vocabulary has a distinct HMM, which is trained using a number of examples of that word. To recognize an unknown word, O, it is scored against all HMM models, \(M_{1,2,3}\) and the HMM model with the highest likelihood score is considered as corresponding model that identifies the word.
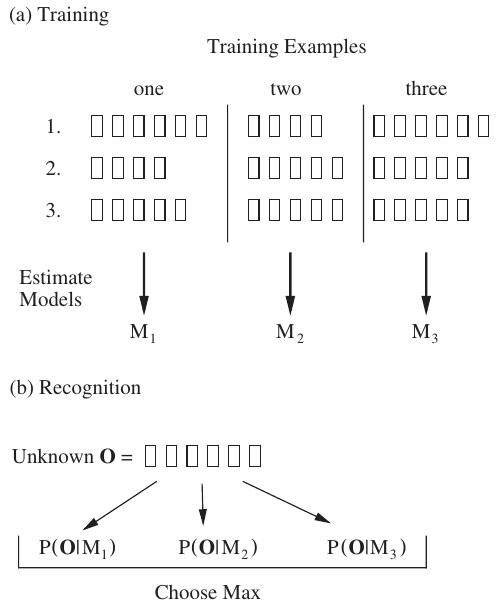
Now, we got the HMM model hence the corresponding sequence of phonemes that represent the unknown word. By looking at the pronunciation dictionary in a reverse way, i.e. phoneme to word, we can find the corresponding word.
Language model
The language model, that computes the prior probability \(P(w)\) for \(w = w_1, \ldots, w_k\), is represented as a n-gram model that models the probability i.e.
\[P(\boldsymbol{w})=\prod_{k=1}^{K} P\left(w_{k} | w_{k-1}, \ldots, w_{1}\right)\]The n-gram probabilities are estimated from the training texts by counting n-gram occurrences. For simplicity, a bi-gram model can be used, in which the probability of a certain word depends only on its previous word i.e. \(P(w_n \mid w_{n-1})\).
The acoustic model, decoder, and language model works together to recognize an unknown audio word or sentence.
References: