Greedy Algorithms
Friday, November 3, 20172 mins read
Let’s say you want to count out a certain amount of money, using the fewest possible number of coins.
Take for example, $6.39, you can choose:
a $5 bill, a $1 bill to make $6, a 25¢ and a 10¢ coin to make $6.35, and four 1¢ to finally make $6.39.
Note that in each step, we took the highest coin value (taking a greedy step) thus reducing the problem to a smaller problem. This paradigm of problem-solving is known as Greedy Algorithms.
A greedy algorithm always makes the choice that looks best at the moment i.e. it makes a locally optimal choice in the hope that this choice will lead to a globally optimal solution.
NOTE: Greedy algorithm do not always yield optimal solutions, but for many problems they do.
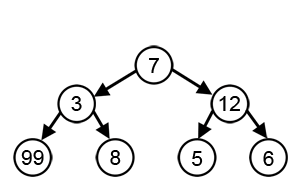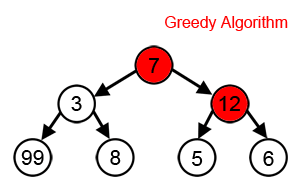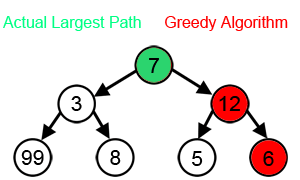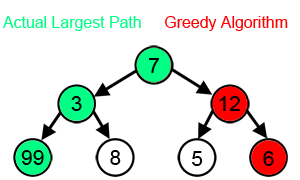
But how can we tell whether a greedy algorithm will solve a particular optimization problem? Most problems for which they work will have two properties:
- Greedy choice property: We can assemble a globally optimal solution by making locally optimal (greedy) choices. It means that we make the choice that looks best in the current problem, without considering results from subproblems.
- Optimal substructure: A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the sub-problems.
Greedy algorithms vs Dynamic programming
In dynamic programming, we make choice at each step, but the choice usually depends on the solutions to subproblems. In a greedy algorithm, we make whatever choice seems best at the moment and then solve the subproblem that remains.
Unlike dynamic programming, which solves the subproblems before making the first choice, a greedy algorithm makes its first choice before solving any subproblems.
In other words, a greedy algorithm never reconsiders its choices.
Algorithms using Greedy algorithm paradigm:
- Dijkstra’s Algorithm for finding shortest path
- Prim’s algorithm for finding Minimum Spanning Trees (MST)
- Huffman coding for data compression
References:
- Greedy algorithms - Wikipedia
- Introduction to algorithms / Thomas H. Cormen . . . [et al.].—3rd ed.
