The Rule of 72: Mathematics in everyday life
Friday, September 29, 20172 mins read
Compound interest is the greatest mathematical discovery of all time. — Albert Einstein
Whenever we borrow money from the bank or any other source, the interest is charged. It may be simple interest or compound interest depending on the conditions.
For example, If you invest $1000 for 10 years at an annual rate of 5%.
With simple interest, $5 is added each year to the principal amount of $1000. Thus, after 10 years, you’ll have $1500.
While with compound interest, if you have P amount at the start of the year, then during the year 5% of P is added. Thus, at the end of the year, you’ll have P(1 + 5/100) amount. This happens every year. Hence, after 10 years, you’ll have $1000(1 + 5/100)100 i.e. $1628.89.
Now, let’s calculate the time required for the principal amount to double. Suppose, you borrow C amount from a bank, on which an annual interst rate of r% is charged, then your debt will double at the time t when
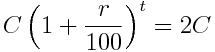
Taking logarithm on both sides and solving, we get
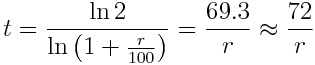
This is known as the rule of 72. If no repayments are made, then at an annual interest rate of r%, it’ll take approx. 72/r years for a debt to double. Also, it you invest money at r% interest rate, then it’ll double in 72/r years.
Although we got the value 69.3, we’re using 72 as it has many small divisors: 1, 2, 3, 4, 6, 12. Thus, it is a good choice for numerator. But, the rule of 72 becomes less accurate at higher interest rates.
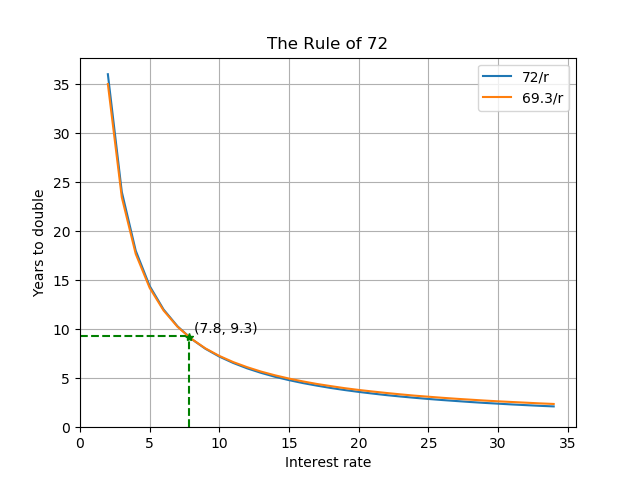
As is clear from the graph, there is a little difference b/w graphs of 69.3/r and 72/r. Thus, the rule of 72 provides a good approximation.
More accurately, the rule underestimates the doubling time when the interest rate is larger than 7.8% and overestimates when the rate is lower than 7.8%. It is the point where the graphs of 72/r and 69.3/r intersects.
Now, we can calculate the time for an amount to double in simple way. For example, when the interest is 6% p.a., we divide 72 by 6, thus, in 12 years, the amount will be doubled. The rule of 72 comes handy in everyday life.
Further Reading: